Falling-Rising Filter

14 mag 2019

Introduction

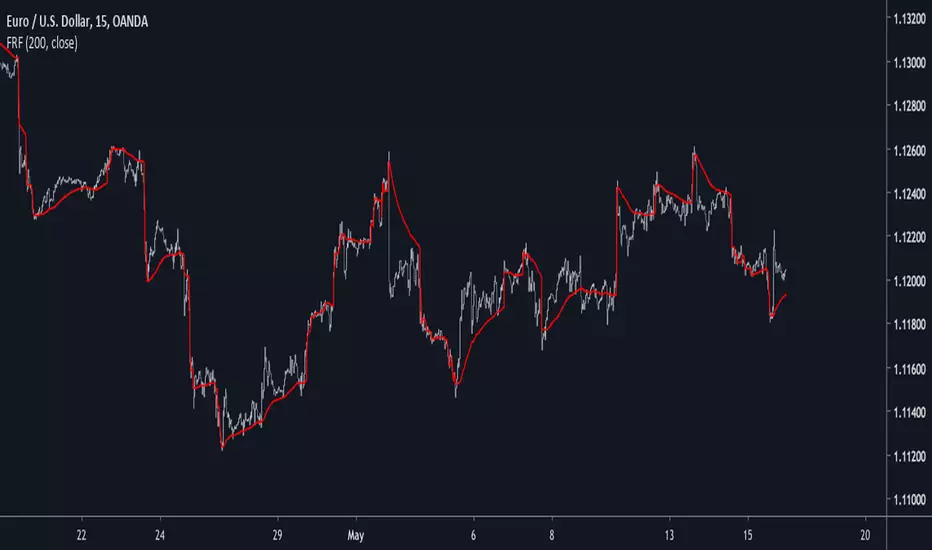
This is a modification of an old indicator i made. This filter aim to adapt to market trend by creating a smoothing constant using highest and lowest functions. This filter is visually similar to the edge-preserving filter, this similarity can make this filter quite good for MA cross strategies.

On The Filter Code

a = nz(a[1]) + alpha*nz(error[1]) + beta*nz(error[1])

The first 3 terms describe a simple exponential filter where error = price - a, beta introduce the adaptive part. beta is equal to 1 when the price is greater or lower than any past price over length period, else beta is equal to alpha, someone could ask why we use two smoothing variable (alpha, beta) instead of only beta thus having :

a = nz(a[1]) + beta*nz(error[1])

well alpha make the filter converge faster to the price thus having a better estimation.



In blue the filter using only beta and in red the filter using alpha and beta with both length = 200, the red filter converge faster to the price, if you need smoother results but less precise estimation only use beta.

Conclusion

I have presented a simple indicator using rising/falling functions to calculate an adaptive filter, this also show that when you create an exponential filter you can use more terms instead of only a = a[1] + alpha*(price - a[1]). I hope you find this indicator useful.

Thanks for reading !

15 mag 2019

Note di rilascio

Fixed a redundant error, thanks to aaahopper for pointing it out.