PINE LIBRARY
Aggiornato FunctionBlackScholes
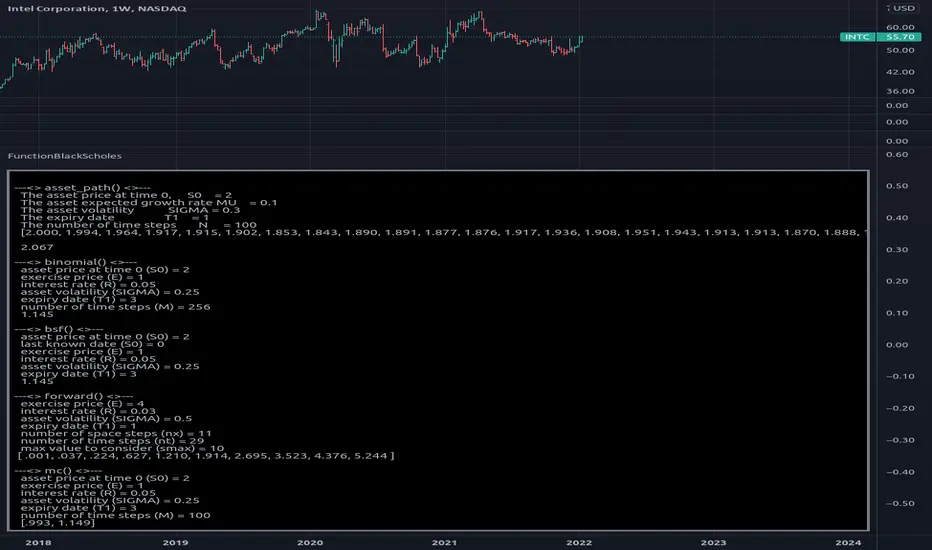
Library "FunctionBlackScholes"
Some methods for the Black Scholes Options Model, which demonstrates several approaches to the valuation of a European call.
// reference:
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.html
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.py
asset_path(s0, mu, sigma, t1, n) Simulates the behavior of an asset price over time.
Parameters:
s0: float, asset price at time 0.
mu: float, growth rate.
sigma: float, volatility.
t1: float, time to expiry date.
n: int, time steps to expiry date.
Returns: option values at each equal timed step (0 -> t1)
binomial(s0, e, r, sigma, t1, m) Uses the binomial method for a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: option value at time 0.
bsf(s0, t0, e, r, sigma, t1) Evaluates the Black-Scholes formula for a European call.
Parameters:
s0: float, asset price at time 0.
t0: float, time at which the price is known.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
Returns: option value at time 0.
forward(e, r, sigma, t1, nx, nt, smax) Forward difference method to value a European call option.
Parameters:
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
nx: int, number of space steps in interval (0, L).
nt: int, number of time steps.
smax: float, maximum value of S to consider.
Returns: option values for the european call, float array of size ((nx-1) * (nt+1)).
mc(s0, e, r, sigma, t1, m) Uses Monte Carlo valuation on a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: confidence interval for the estimated range of valuation.
Some methods for the Black Scholes Options Model, which demonstrates several approaches to the valuation of a European call.
// reference:
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.html
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.py
asset_path(s0, mu, sigma, t1, n) Simulates the behavior of an asset price over time.
Parameters:
s0: float, asset price at time 0.
mu: float, growth rate.
sigma: float, volatility.
t1: float, time to expiry date.
n: int, time steps to expiry date.
Returns: option values at each equal timed step (0 -> t1)
binomial(s0, e, r, sigma, t1, m) Uses the binomial method for a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: option value at time 0.
bsf(s0, t0, e, r, sigma, t1) Evaluates the Black-Scholes formula for a European call.
Parameters:
s0: float, asset price at time 0.
t0: float, time at which the price is known.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
Returns: option value at time 0.
forward(e, r, sigma, t1, nx, nt, smax) Forward difference method to value a European call option.
Parameters:
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
nx: int, number of space steps in interval (0, L).
nt: int, number of time steps.
smax: float, maximum value of S to consider.
Returns: option values for the european call, float array of size ((nx-1) * (nt+1)).
mc(s0, e, r, sigma, t1, m) Uses Monte Carlo valuation on a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: confidence interval for the estimated range of valuation.
Note di rilascio
v2 fixed some issues.Libreria Pine
Nello spirito di TradingView, l'autore ha pubblicato questo codice Pine come libreria open source affinché altri programmatori della nostra comunità possano riutilizzarlo. Complimenti all'autore! È possibile utilizzare questa libreria privatamente o in altre pubblicazioni open source, ma il riutilizzo di questo codice nelle pubblicazioni è soggetto al Regolamento.
Declinazione di responsabilità
Le informazioni e le pubblicazioni non sono intese come, e non costituiscono, consulenza o raccomandazioni finanziarie, di investimento, di trading o di altro tipo fornite o approvate da TradingView. Per ulteriori informazioni, consultare i Termini di utilizzo.
Libreria Pine
Nello spirito di TradingView, l'autore ha pubblicato questo codice Pine come libreria open source affinché altri programmatori della nostra comunità possano riutilizzarlo. Complimenti all'autore! È possibile utilizzare questa libreria privatamente o in altre pubblicazioni open source, ma il riutilizzo di questo codice nelle pubblicazioni è soggetto al Regolamento.
Declinazione di responsabilità
Le informazioni e le pubblicazioni non sono intese come, e non costituiscono, consulenza o raccomandazioni finanziarie, di investimento, di trading o di altro tipo fornite o approvate da TradingView. Per ulteriori informazioni, consultare i Termini di utilizzo.